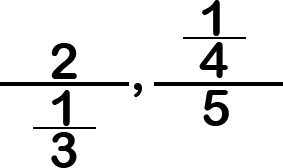গণিত আসলে একটি মজার বিষয়। যারা গণিত রপ্ত করে নিয়েছে তারা অনেক কিছুই পারে। কিন্তু অংক করতে বসে আমরা অনেকেই বিষয়টিকে জটিল বানিয়ে ফেলি। ফলে বেশিরভাগ শিক্ষার্থীদের কাছেই গণিত কঠিন মনে হয়। গণিতে ভাল করার জন্য আমাদেরকে আগে গণিতের Basic Rule গুলো ভাল করে জানতে হবে। আজ এখান থেকে গণিতের কিছু খুটিনাটি বিষয় জেনে নিন। এগুলো আপনাকে অংক করার সময় অনেকটাই সাহায্য করবে।
গণিতের বেসিক কিছু প্রশ্ন-Basic Rules of Mathematics
🎯 অঙ্ক কী? (What is Digit?)
অঙ্কঃ গণিতের যাবতীয় সংখ্যা শেখার জন্য কতকগুলো প্রতীক বা চিহ্ন ব্যবহার করা হয়। যেসব প্রতীক বা চিহ্ন ব্যবহার করা হয় সেগুলোকে অঙ্ক বলে। ০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯-এই দশটি চিহ্নের প্রত্যেকটি এক একটি অঙ্ক। সংখ্যা তৈরির মূল উপাদান হলো “অঙ্ক”। অঙ্কের কাজই হলো সংখ্যা তৈরি করা। অঙ্ক দুই ধরনের। যথা:
(ক) সাথর্ক অঙ্কঃ ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯।
(খ) সহকারী অঙ্কঃ ০ (শূন্য)।
🎯 সংখ্যা কী? (What is Numbers?)
সংখ্যাঃ অঙ্ক ও সংখ্যা এক নয়। সব অঙ্কই সংখ্যা, কিন্তু সব সব সংখ্যাই অঙ্ক নয়। দশটি (০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯) অঙ্কসহ আরো কতকগুলি চিহ্নের (যেমন- দশমিক বিন্দু, বর্গ, বর্গমূল ইত্যাদি) সাহায্যে যা তৈরি হয়, তাকে সংখ্যা বলে। যেমন- ৫ একাধারে একটি অঙ্ক ও সংখ্যা, কিন্তু ৫৫৫ হলো তিন অঙ্কবিশিষ্ট একটি সংখ্যা।
লব ও হরঃ সংখ্যা সম্পর্কে বিস্তারিত জানার পূর্বে আসুন ভগ্নাংশের লব ও হর সম্পর্কে কেবল দুটো কথা জেনে নিই। ধরুন, আমি একটি ভগ্নাংশ লিখলাম এখানে 4 হলো লব আর 5 হলো হর। অর্থাৎ ভগ্নাংশের উপরের সংখ্যাটিকে বলে “লব” এবং নিচের সংখ্যাটিকে বলে “হর”। আশা করি বুঝতে পেরেছেন।
সংখ্যার প্রকারভেদ (Classification of Numbers): সংখ্যা প্রধানত দুই প্রকার। যথাঃ (ক) বাস্তব সংখ্যা ও (খ) কাল্পনিক সংখ্যা।
📌(ক) বাস্তব সংখ্যা কাকে বলে? (What is the definition of Real Numbers?)
বাস্তব সংখ্যাঃ যে সকল সংখ্যাকে সংখ্যারেখার মাধ্যমে প্রকাশ করা যায়, তাদেরকে বাস্তব সংখ্যা বলে। সকল মূলদ ও অমূলদ সংখ্যাকে বাস্তব সংখ্যা বলা হয়। অর্থাৎ সকল ধনাত্মক সংখ্যা, ঋণাত্মক সংখ্যা ও শূন্য সবই বাস্তব সংখ্যার সদস্য। যেমন- ১, ৪, ৮, ০, -২, -৯,, ০.২৩, ০.৯৬ ইত্যাদি। বাস্তব সংখ্যার সেটকে সাধারণত R দ্বারা প্রকাশ করা হয়। নিম্নে আমরা বাস্তব সংখ্যা নিয়ে বিস্তারিত আলোচনা করব।
ফেসবুক থেকে ভগ্নাংশের সংখ্যাগুলো দেখতে সমস্যা হলে অন্য যেকোন ব্রাউজার দিয়ে দেখুন, সমস্যা হবেনা।
📌(খ) কাল্পনিক সংখ্যা কাকে বলে? (What is the definition of Imaginary Numbers?)
কাল্পনিক সংখ্যাঃ যেসব সংখ্যার বাস্তব কোনো অস্তিত্ব নেই, তাদেরকে অবাস্তব সংখ্যা অর্থাৎ কাল্পনিক সংখ্যা বলে। আমরা জানি, ঋণাত্মক কোনো সংখ্যার বর্গমূলের কোনো অস্তিত্ব নেই, এই ধরনের সংখ্যাকে কাল্পনিক সংখ্যা বলে। যেমন: – , –
ইত্যাদি। কাল্পনিক সংখ্যার সেটকে সাধারণত i দ্বারা প্রকাশ করা হয়। যেমন, i= –
★ জটিল সংখ্যা কাকে বলে? (What is the definition of Complex Numbers?)
জটিল সংখ্যাঃ বাস্তব সংখ্যা ও কাল্পনিক সংখ্যার সমন্বয়ে যে সংখ্যা গঠিত হয় তাকে জটিল সংখ্যা বলে। অর্থাৎ a ও b বা, x ও y বাস্তব সংখ্যা হলে aib বা, x
iy আকারকে জটিল সংখ্যা বলে। জটিল সংখ্যার সেটকে Z বা C দ্বারা প্রকাশ করা হয়।
আসুন, এখন বাস্তব সংখ্যা সম্পর্কে বিস্তারিত জেনে নিইঃ
বাস্তব সংখ্যার প্রকারভেদ (Classification of Real Numbers): বাস্তব সংখ্যাও আবার দুই ভাগে বিভক্ত। যথাঃ i) মূলদ সংখ্যা ও ii) অমূলদ সংখ্যা।
📌 i) মূলদ সংখ্যা কী? (What is Rational Numbers?)
মূলদ সংখ্যাঃ যেসব সংখ্যাকে ভগ্নাংশ আকারে প্রকাশ করা যায়, তাদেরকে মূলদ সংখ্যা বলে। যেখানে p ও q পূর্ণসংখ্যা এবং q≠0 হলে, আকারের সংখ্যাকে মূলদ সংখ্যা বলে। যেমন:
=3,
=5.5 ইত্যাদি মূলদ সংখ্যা। মূলদ সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাত হিসেবে প্রকাশ করা যায়। সুতরাং সকল পূর্ণসংখ্যা ও সকল ভগ্নাংশ সংখ্যা হলো মূলদ সংখ্যা। মূলদ সংখ্যাকে Q দ্বারা প্রকাশ করা হয়।
📌 ii) অমূলদ সংখ্যা কী? (What is Irrational Numbers?)
অমূলদ সংখ্যাঃ যেসব সংখ্যাকে ভগ্নাংশ আকারে প্রকাশ করা যায় না, তাদের অমূলদ সংখ্যা বলে। যেখানে p ও q পূর্ণসংখ্যা এবং q≠0 হলে, যে সংখ্যাকে আকারে প্রকাশ করা যায় না তাকে অমূলদ সংখ্যা বলে। অমূলদ সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাত হিসেবে প্রকাশ করা যায় না। যেমন:
,
ইত্যাদি।
📌 দশমিক ভগ্নাংশ সংখ্যাঃ মূলদ ও অমূলদ সংখ্যাকে দশমিকে প্রকাশ করা হলে তাকে দশমিক ভগ্নাংশ বলা হয়। প্রত্যেক বাস্তব সংখ্যাকে দশমিক ভগ্নাংশে প্রকাশ করা যায়। যেমন: 3=3.0, =2.5,
=3.333…..,
=1.732….. ইত্যাদি। দশমিক ভগ্নাংশ ৩ প্রকার। যথা: সসীম দশমিক ভগ্নাংশ, আবৃত্ত দশমিক ভগ্নাংশ ও অসীম দশমিক ভগ্নাংশ।
📌 সসীম দশমিক ভগ্নাংশঃ সসীম দশমিক ভগ্নাংশে দশমিক চিহ্নের ডানদিকে সসীম সংখ্যক অঙ্ক থাকে। যেমন: 0.12, 2.023, 4.832, 77.9686 ইত্যাদি সসীম দশমিক ভগ্নাংশ।
📌 আবৃত্ত দশমিক ভগ্নাংশঃ আবৃত দশমিক ভগ্নাংশে দশমিক চিহ্নের ডানদিকের অঙ্কগুলো বা অংশবিশেষ বারবার থাকবে। যেমন: 3.333…., 2.454545…., 5.890890… ইত্যাদি আবৃত্ত দশমিক ভগ্নাংশ।
বিষয়টি পুরোপুরি জেনে নিতে আবার বলতে হয়, যে সকল দশমিক ভগ্নাংশে দশমিক বিন্দুর ডানে একটি অঙ্ক ক্রমান্বয়ে বারবার বা একাধিক অঙ্ক পর্যায়ক্রমে বারবার আসে, এদের আবৃত্ত দশমিক ভগ্নাংশ বলা হয়। আবৃত্ত বা পৌনঃপুনিক দশমিক ভগ্নাংশে যে অংশ বারবার অর্থাৎ পুনঃপুন আবির্ভূত হয়, একে আবৃত্ত অংশ বলে। আবৃত্ত দশমিক ভগ্নাংশে একটি অঙ্ক আবৃত্ত হলে, সে অঙ্কের উপর পৌনঃপুনিক বিন্দু এবং একাধিক অঙ্ক আবৃত্ত হলে, কেবল প্রথম ও শেষ অঙ্কের উপর পৌনঃপুনিক বিন্দু দেওয়া হয়। যেমন: 3.5555….. কে লেখা হয় 2.দ্বারা এবং 3.124124…. কে লেখা হয়, 3.
2
দ্বারা।
📌 অসীম দশমিক ভগ্নাংশঃ অসীম দশমিক ভগ্নাংশে দশমিক চিহ্নের ডানদিকের অঙ্ক কখনো শেষ হয় না, অর্থাৎ দশমিক চিহ্নের ডানদিকের অঙ্কগুলো সসীম হবে না বা অংশবিশেষ বারবার আসবে না। যেমন: 1.4142135….., 2.8284271…. ইত্যাদি অসীম দশমিক ভগ্নাংশ।
অসীম দশমিক ভগ্নাংশ দুই প্রকার। যথা: অসীম আবৃত্ত দশমিক ভগ্নাংশ ও অসীম অনাবৃত্ত দশমিক ভগ্নাংশ।
মনে রাখবেন, দশমিক বিন্দুর সংখ্যা সসীম হলে মূলদ সংখ্যা আর দশমিক বিন্দুর সংখ্যা অসীম হলে সেটা অমূলদ সংখ্যা।
মূলদ সংখ্যার প্রকারভেদ (Classification of Rational Numbers): মূলদ সংখ্যাকে দুইভাগে ভাগ করা যায়। যথাঃ A) পূর্ণসংখ্যা ও B) ভগ্নাংশ।
📌 A) পূর্ণসংখ্যা কী? (What is Integers?)
পূর্ণসংখ্যাঃ যে সমস্ত সংখ্যার কোন ভগ্নাংশ থাকে না তাদেরকে পূর্ণসংখ্যা বলে। শূন্যসহ সকল ধনাত্মক ও ঋণাত্মক অখন্ড সংখ্যাসমূহকে পূর্ণসংখ্যা বলা হয়। পূর্ণসংখ্যার সংখ্যা অসীম। ধনাত্মক পূর্ণসংখ্যা, ঋণাত্মক পূর্ণসংখ্যা এবং শূন্য এই তিনরকম ধরনের সংখ্যাগুলিকে সবমিলিয়ে বলা হয় পূর্ণসংখ্যা। যেমন, -3, -2, -1, 0, 1, 2, 3 ইত্যাদি। পূর্ণসংখ্যার সেটকে Z দ্বারা প্রকাশ করা হয়।
পাটিগণিতের সকল শর্টকাট PDF Download করতে এখানে ক্লিক করুন।
পূর্ণসংখ্যার শ্রেণিবিভাগ (Classifications of Integers): পূর্ণসংখ্যাকে সাধারণত দুটি ভাগে ভাগ করা হয়েছে। যথা: ১) ধনাত্মক সংখ্যা ও ২) ঋণাত্মক সংখ্যা।
১) ধনাত্মক সংখ্যা কি? (What is Positive Numbers?)
ধনাত্মক সংখ্যাঃ শূন্য অপেক্ষা বড় সকল বাস্তব সংখ্যাকে ধনাত্মক সংখ্যা বলে। যেমন: 1, 3, ,
,
, 0.415, 4.12076 ইত্যাদি ধনাত্মক সংখ্যা।
২) ঋণাত্মক সংখ্যা কি? (What is Negative Numbers?)
ঋণাত্মক সংখ্যাঃ শূন্য অপেক্ষা ছোট সকল বাস্তব সংখ্যাকে ঋণাত্মক সংখ্যা বলে। যেমন: -1, -3, –, –
, –
,-0.415, -4.12076 ইত্যাদি ঋণাত্মক সংখ্যা।
এছাড়া অঋণাত্মক সংখ্যাও রয়েছে।
📌 অঋণাত্মক সংখ্যা কি? (What is Non-negative Numbers?)
অঋণাত্মক সংখ্যাঃ শূন্যসহ সকল ধনাত্মক সংখ্যাকে অঋণাত্মক সংখ্যা বলা হয়। যেমন: 0, 1, 3, ,
,
, 0.415, 4.12076 ইত্যাদি অঋণাত্মক সংখ্যা।
ধনাত্মক সংখ্যাকেই অঋণাত্মক সংখ্যা বলে। ধনাত্মক সংখ্যায় (0) শূন্য নেই, কিন্তু অঋণাত্মক সংখ্যায় (0) শূন্য ও ধনাত্মক সংখ্যা উভয়ই রয়েছে। অঋণাত্মক সংখ্যাকে দুই ভাগে ভাগ করা হয়েছে। যেমন: শূন্য (0) ও স্বাভাবিক সংখ্যা। আসুন স্বাভাবিক সংখ্যা কি সেটা জেনে নিইঃ
>) স্বাভাবিক সংখ্যা কী? (What is Natural Numbers?)
স্বাভাবিক সংখ্যাঃ ধনাত্মক পূর্ণসংখ্যাকে স্বাভাবিক সংখ্যা বা প্রাকৃতিক সংখ্যা বলে। অর্থাৎ শূন্য (0) ব্যতীত 1, 2, 3, 4, 5, 6………. ইত্যাদি সংখ্যাগুলোকে স্বাভাবিক সংখ্যা বলে। স্বাভাবিক সংখ্যার সেটকে N দ্বারা প্রকাশ করা হয়। যেমন: N= {1, 2, 3, 4, 5……} ইত্যাদি।
স্বাভাবিক সংখ্যাকে দুইভাবে ভাগ করা যায়। যথাঃ i) মৌলিক সংখ্যা ও ii) যৌগিক সংখ্যা।
📌 i) মৌলিক সংখ্যা কাকে বলে? (What is the definition of Prime Numbers?)
মৌলিক সংখ্যাঃ যে সকল স্বাভাবিক সংখ্যাকে কেবল সেই সংখ্যা এবং 1 ব্যতীত অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না তাকে মৌলিক সংখ্যা বলে। মৌলিক সংখ্যায় 1 এবং ঐ সংখ্যা ছাড়া অন্য কোনো গুণনীয়ক নেই অথবা নিঃশেষে বিভাজ্য নয়। মনে রাখবেন, মৌলিক সংখ্যার কোনো প্রকৃত উৎপাদক নেই। মৌলিক সংখ্যার সেটকে সাধারণত P দ্বারা প্রকাশ করা হয়। যেমন: P= {2, 3, 5, 7, 11, 13………..} ইত্যাদি। উল্লেখ্য যে, একমাত্র 2 হচ্ছে জোড় মৌলিক সংখ্যা।
📌 ii) যৌগিক সংখ্যা কাকে বলে? (What is the definition of Composite Numbers?)
যৌগিক সংখ্যাঃ যে সকল স্বাভাবিক সংখ্যার (সেই সংখ্যা ও 1 ব্যতীত) কমপক্ষে একটি প্রকৃত উৎপাদক থাকে, তাকে যৌগিক সংখ্যা বলে। যৌগিক সংখ্যায় 1 এবং ঐ সংখ্যা ছাড়া অন্তত একটি গুণনীয়ক থাকে এবং সংখ্যাটি নিঃশেষে বিভাজ্য। যৌগিক সংখ্যার সেটকে সাধারণত P’ দ্বারা প্রকাশ করা হয়। যেমন: P’= {4, 6, 8, 9, 14, 15………..} ইত্যাদি।
[বি.দ্র. 1 মৌলিক এবং যৌগিক সংখ্যা কোনোটিই নয়।]
ভগ্নাংশ-Fraction
B) ভগ্নাংশ কী? (What is Fraction?)
ভগ্নাংশঃ কোনো বস্তু বা পরিমাণের অংশ নির্দেশ করতে যে সংখ্যা শ্রেণি ব্যবহৃত হয়, তাকে ভগ্নাংশ বলে। অর্থাৎ একটি বস্তুকে কয়েকটি সমান অংশে বিভক্ত করে তার কতগুলো অংশ নেয়া হলে তা প্রকাশ করার মাধ্যম হলো ভগ্নাংশ। যেমন: ,
,
, ইত্যাদি।
ভগ্নাংশের শ্রেণিবিভাগ (Classifications of Fraction): ভগ্নাংশকে ৩টি অনুসারে ভাগ করা যায়। যেমনঃ ১) প্রকৃতি অনুসারে, ২) আকৃতি অনুসারে, ৩) হর অনুসারে।
🎯১) প্রকৃতি অনুসারেঃ প্রকৃতি অনুসারে ভগ্নাংশ ৩ প্রকার। যথা: ক) প্রকৃত ভগ্নাংশ, খ) অপ্রকৃত ভগ্নাংশ ও গ) মিশ্র ভগ্নাংশ।
ক) প্রকৃত ভগ্নাংশ কী? (What is Proper Fraction?)
প্রকৃত ভগ্নাংশঃ যে ভগ্নাংশের হর অপেক্ষা লব ছোট তাকে প্রকৃত ভগ্নাংশ বলে। যেমন: ,
ইত্যাদি।
খ) অপ্রকৃত ভগ্নাংশ কী? (What is Improper Fraction?)
অপ্রকৃত ভগ্নাংশঃ যে ভগ্নাংশের হর অপেক্ষা লব বড় তাকে অপ্রকৃত ভগ্নাংশ বলে। যেমন: ,
ইত্যাদি।
গ) মিশ্র ভগ্নাংশ কী? (What is Mixed Fraction?)
মিশ্র ভগ্নাংশঃ যে ভগ্নাংশ পূর্ণসংখ্যার সাথে যুক্ত থাকে তাকে মিশ্র ভগ্নাংশ বলে। যেমন: ,
ইত্যাদি।
🎯২) আকৃতি অনুসারেঃ আকৃতি অনুসারেও ভগ্নাংশকে ৩ ভাগে ভাগ করা যায়। যথা: ক) সরল ভগ্নাংশ, খ) জটিল ভগ্নাংশ ও গ) যৌগিক ভগ্নাংশ।
ক) সরল ভগ্নাংশ কী? (What is Simple Fraction?)
সরল ভগ্নাংশঃ যে ভগ্নাংশে শুধু স্বাভাবিক সংখ্যার হর ও লব থাকে, তাকে সরল ভগ্নাংশ বলে। যেমন: ,
ইত্যাদি।
খ) জটিল ভগ্নাংশ কী? (What is Complex Fraction?)
জটিল ভগ্নাংশঃ হর কিংবা লব উভয়ই বা যেকোনো একটি সরল ভগ্নাংশ দ্বারা গঠিত হলে তাকে জটিল ভগ্নাংশ বলে। যেমন:
গ) যৌগিক ভগ্নাংশ কী? (What is Compound Fraction?)
যৌগিক ভগ্নাংশঃ যে ভগ্নাংশের হর ও লব উভয়ে কিংবা যে কোনো একটিতে নির্দিষ্ট কার্যবিধি থাকে তাকে যৌগিক ভগ্নাংশ বলে। যেমন:
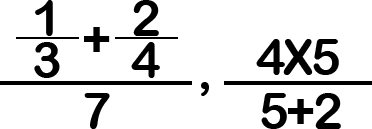 বাংলা, সাধারণ জ্ঞান এবং গণিতের সকল শর্টকাট টেকনিক এর PDF ডাউনলোড করুন
বাংলা, সাধারণ জ্ঞান এবং গণিতের সকল শর্টকাট টেকনিক এর PDF ডাউনলোড করুন
🎯৩) হর অনুসারেঃ হরের উপর ভিত্তি করে ভগ্নাংশকে দুইভাগে ভাগ করা হয়েছে। যথাঃ ক) সমহর বিশিষ্ট ভগ্নাংশ ও খ) অসমহর বিশিষ্ট ভগ্নাংশ।
ক) সমহর বিশিষ্ট ভগ্নাংশ কী?
সমহর বিশিষ্ট ভগ্নাংশঃ একই হরবিশিষ্ট ভগ্নাংশকে সমহর বিশিষ্ট ভগ্নাংশ বলে। যেমন:,
,
ইত্যাদি।
খ) অসমহর বিশিষ্ট ভগ্নাংশ কী?
অসমহর বিশিষ্ট ভগ্নাংশঃ বিভিন্ন ধরনের হরবিশিষ্ট ভগ্নাংশকে অসমহর বিশিষ্ট ভগ্নাংশ বলে। যেমন: ,
ইত্যাদি।